Y. H. Hu 1*, R. Rouvier2, J. P. Poivey2,4, H. C. Liu1, and C. Tai3
1 Livestock Research Institute, ILAN Branch, Council of Agriculture, WuChieh, Ilan 268, Taiwan, Republic of China
2 Institut National de la Recherche Agronomique, Station d’Amélioration Génétique des Animaux, Centre de Recherches de Toulouse, BP 52627, F31326 Castanet-Tolosan Cedex, France
3 National Science Council, Taipei, 106 Taiwan, Republic of China
4 CIRAD, Campus International de Baillarguet, 34000 Montpellier, France
* Corresponding author, E-mail: hueliao@ms36.hinet.net
ABSTRACT
Under the Cooperation program between INRA and LRI-COA, the line L302 of Muscovy was established at DRC (Duck Research Center) in 1984 from 80 eggs donated by a French farmer. The population is kept closed and moderately selected for body weight at 10 weeks of age. It was conducted in three different periods: period I (G0 to G8), period II (G8-G13), and period III (G13-15), according to the methods of selection used.
During the period I, 12 males and 11 females were selected to constitute the parents of the line 302. The selection of phenotypic body weight at ten weeks of age in both sexes was carried out in the first stage. At the second stage, the ducks were selected according to the reproductive abilities and body weight. The genetic parameters were estimated from this base population.
During the period II, the prediction of the additive genetic values were used as a criterion in replacement of the phenotypic body weight and a control line (CL) and a selection line (SL) were created since 1997. 18 males and 87 females of G8 were selected to constitute the parents of SL, 13 males and 47 females were chosen to constitute the parents of CL. In the SL line, the ducks were selected in a first step, within sire family, by truncation of superior values of the BLUP animal model for the body weight at 10 weeks of age, using the male breeding value (GBW10m) both in male and female ducks. In a second step the ducks were selected according to their reproductive abilities. In the CL line, the ducks where chosen within sire families when their breeding values were near the mean of the population in G8 and G9 and they were randomly chosen from G10 to G13.
During the period III, due to the negative genetic correlations found between the growth traits and egg production, a new criterion was studied and an index combining two characters and their weighting coefficients was used for selection. To obtain the weighting coefficients a0 and a1 of this index, we used the classical theory on the prediction of the genetic trend, and estimated the variances and covariances of the traits from the data of G13 and G14. This criterion was applied since 2004, and the efficiency of the new selection method is currently worth to estimate.
KEY WORDS
: Muscovy, Selection, Additive genetic value, Body weight, Laying performance, Index.
INTRODUCTION
In Taiwan, for 30 years the Muscovy have been used as terminal sires in 3-way crossbreeding by artificial insemination of the common duck female as well as in pure breeding for Muscovy. Consequently, a Muscovy experimental line L302 was established in the Duck Research Center (DRC, I-Lan Branch) of the Livestock Research Institute in 1984 in order to study the possibilities of genetic improvement (Tai, 1985; Tai et al., 1987). It was reared in a closed small-sized strain. The body weight at 10 and 18 weeks of age, and the feather length at 10 weeks of age were measured. The reproductive performances traits were individually recorded.
Taiwan is a subtropical island (in latitude 22-25º and longitude 120-122º), with averaged monthly temperatures 18-24º in winter and 22-34ºC in the other seasons, and with high Relative Humidity (RH=73%-87%) in the plains. In Ilan where the DRC is situated, it was much more humid. The average relative humidity was 84% from 1971 to 2000, it was less humid in summer (81%-82%) and 86% in autumns in Ilan. Most of the duck house in Taiwan is opened or in semi-confinement. Not much was known about the climatic effect on the growth in Muscovy duck.
The feeding program has been described by Hu (1999). There were some modifications of feeding program in the growing period from G0 to G6. The feeding program was then kept unchanged.
Purpose is to discuss the results got along three successive periods of 15 generations of selection studies.
MATERIALS AND METHODS
Under the Cooperation program between INRA and LRI-COA, the line L302 of Muscovy was established at the DRC in 1984 from 80 eggs donated by a French farmer and was then selected to improve the growth performance (Tai, 1986). The population was kept closed. The average generation interval was 18 months. The eggs hatched in several batches in each generation. In each batch, they were stored at a temperature of about 18ºC for a maximum holding time of 14 days. The ducklings were raised until 3 weeks of age on a wire floor. After 3 weeks, they were raised in half opened (semi-confinement) housing with uninsulated sidewall. After 10 weeks, the selected males and females were kept in individual cages, as described by Hu et al. (1993). As there is a large degree of body weight sexual dimorphism, using Falconer's approach (1952), the measures obtained in males and females were considered as different traits. Six traits were individually measured and recorded on the growing birds: male and female body weight at 10 and 18 weeks of age, length of the 8th primary feather for males and females at 10 weeks of age (BW10m, BW10f, BW18m, BW18f, FL10m, and FL10f, respectively). The duck laying traits were also individually measured. The program proceeded in three different steps, period I (G0 to G8), period II (G8-G13), and period III (G13-15), according to the methods of selection used.
Period I: Selection based on phenotypic performance and estimation of genetic parameters from G0 to G8
Generation 0 (G0) of the line L302 started with 27 drakes and 11 females among which 12 drakes and 11 females were parents of the generation 1 (G1). A mild selection pressure was applied on individual phenotypic values. The goal of this first period was thus to estimate the heritabilities and genetic correlations of the measured traits in male and female Muscovy ducklings bred in Taiwanese climatic conditions. In these first generations, there was not any control line to evaluate the realized genetic progress.
The structure of the selection experiment is described in Table 1 for numbers of ducks (males and females) and the hatching date of each generation. The selection intensity was higher in males than in females. The selection was done in two steps: at first, males and females were individually selected according to their body weight at 10 weeks of age. The males were selected when BW10m was superior to the hatch average. In generation 4 and 5, the females with BW10f within the mean ± 1 phenotypic standard deviation (sd) were selected. In the other generations, the females with BW10f heavier than one sd below the mean were selected. Secondly, after the ducks selected in first step of individual selection had reached maturity, the males were selected within the sire family according to their ability to give semen for artificial insemination and their body weight at 10 weeks of age. The laying females were randomly chosen to be dams of the next generation. The sires and dams were mated by artificial insemination, avoiding any full and half- sib mating.
Table 1. Structure of the selected experimental line
Generation number | Number of hatches | Hatch period | Number of offspring males females | Number of parents(1)
males females |
0 1 2 3 4 5 6 7 8 Total | 1 17 15 6 7 5 7 8 6 72 | 21/05/84 22/04/85-29/10/85 05/11/86-28/05/87 04/07/88-08/08/88 08/08/90-18/09/90 02/09/91-30/09/91 14/06/93-19/07/93 06/09/94-12/10/94 20/05/95-12/06/95 03/06/96-08/08/96 | 27 91 406 574 525 528 430 166 235 394 3375 | 11 96 429 463 579 639 406 151 230 364 3369 | 12 9 18 20 23 15 14 19 - 130 | 11 57 124 125 141 101 103 112 - 774 |
(1) Parents of offspring in the next generation.
Statistical analysis
All records were analysed using the SAS univariate procedure (SAS Institute Inc., 1994), to calculate means and phenotypic standard deviations (sd) and to test for normality of the distributions using the Shapiro-Wilk test by sex and by generation. Some extreme and abnormal data (54 out of 6626) were discarded (when they were less than the generation mean minus 3 sd).
A multivariate analysis with an animal model of BW10m, BW10f, BW18m, BW18f, Fl10m, Fl10f was performed, using the model:
yij=hi+aj+eij
where yij was the performance of the jth animal (j=1,n where n is the total number of animals which was equal to 6572) born in the ith hatch, hi was the fixed effect of the ith hatch (the total number of hatches was equal to 72), aj (j=1, n) the random additive genetic effect of the jth animal, eij the random residual term. The latter two effects were assumed to be normally distributed. With that model the dam effect is only in the residual.
Heritabilities and genetic correlations of 6 characters were estimated by the restricted maximum likelihood method (REML) applied to an animal model. The VCE 3.2 package developed by Groeneveld (1994a and b ; 1996) was used. The computing strategy was the same as in Cheng et al. (1995). Male and female measurements were considered as different traits. According to the animal model, all the pedigree information was taken into account. Furthermore, accounting for inbreeding in the relationship matrix prevented underestimation of genetic variances (Tixier-Boichard et al., 1995). The coefficient of inbreeding was calculated by a program using the method of Van Raden (1992) and written by Boichard (1998).
Heritabilities of sexual dimorphism measured by the difference between male and female performances for the same trait at the same age (Δp) were calculated according to Chapuis et al. (1996) as :

where , , , were the additive genetic variances or covariances of various traits in male, in female and between male and female respectively and , , were the residual variances or covariances of various traits in male and in female, respectively. 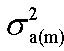


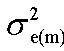


Using these genetic parameters of these traits estimated in the base population, the predicted individual genetic values of 6 characters were estimated all together by Pest 3.1 package (Groeneveld and Kovac, 1990), with BLUP applied to an animal model, with a performance file of 7372 animals from G1 to G8, a pedigree file of 8947 animals, by means of Gauss-Seidel iteration for animal effects. The inbreeding coefficients were considered for the additive relationship matrix. For each generation, the means predicted genetic values of each traits were calculated in order to evaluate the genetic trends over the eight generations of selection (Hu et al.1999).
Period II: Selection based on the additive genetic values and setting up a control line
During the period II, the predicted additive genetic values of body weight at ten weeks of age were used as selection criterion. The goal of this study was thus to analyze the response to selection for an increased body weights at 10 weeks of age in the first five generations of the selection experiment. This new experiment was established in 1997 with animals of the generation 8 (G8) of the former selection experiment. The number of ducks involved as parents and in individual performance test in G8 up to G13, the selection differentials on breeding values of body weight at 10 weeks of age in the selected line (LS) and the control or unselected line (LC), is shown in Table 2.
Table 2. The experimental population for the selection
Generation | Line | Hatch | Hatch period | Ducks | Parents | S.D |
G8 | SL | 4 | 11/06/97-22/07/97 | 476 | M=18 | 62 |
| | | | 504 | F=87 | 63 |
| CL | | | | M=13 | 29 |
| | | | | F=47 | -14 |
G9 | SL | 2 | 20/07/98-27/07/98 | M=341 | M=19 | 4 |
| | | | F=311 | F=97 | 17 |
| CL | | | M=116 | M=10 | 15 |
| | | | F=158 | F=36 | 23 |
G10 | SL | 4 | 19/06/00-10/07/00 | M=532 | M=23 | 68 |
| | | | F=509 | F=96 | 33 |
| CL | | | M=178 | M=10 | 35 |
| | | | F=186 | F=27 | -6 |
G11 | SL | 5 | 06/08/01-03/09/01 | M=309 | M=21 | 62 |
| | | | F=360 | F=97 | 25 |
| CL | | | M=91 | M=10 | -27 |
| | | | F=76 | F=29 | 17 |
G12 | SL | 3 | 07/29/02-08/12/02 | M=419 | M=18 | 79 |
| | | | F=401 | F=75 | 71 |
| CL | | | M=134 | M=10 | 13 |
| | | | F=132 | F=31 | 8 |
G13 | SL | 3 | 08/18/03-09/03/03 | M=264 | | |
| | | | F=208 | | |
| | | | M=93 | | |
| | | | F=102 | | |
Hatch: number of batch of hatch, which is the same for SL and CL;
Ducks: the number of measured ducks; Parents: the number of selected or chosen parents;
M: male; F: female
SL: Selection line; CL: Control line
SD: Selection differential on predicted breeding values in the SL and CL lines
In order to take into account the environmental variations and to estimate the selection response (Hill, 1972), a control line (CL) and a selected line (SL) were created since G8 in 1997. There were four hatches between June 11 and July 22, 1997, in G8. Four hundred seventy six males and 504 females were individually measured and data were recorded. Among these ducks, 18 males and 87 females were selected to constitute the parents of the selected line (SL), 13 males and 47 females were chosen to constitute the parents of control or unselected line (CL). Both lines were maintained at the same time under standardized conditions at the DRC. The management was described in Hu et al. (1993), Hu (1999) and Hu et al. (2004). In the SL line, male and female ducks in each generation were selected in a first step, within sire families, by truncation of superior values of the BLUP animal model for the body weight at 10 weeks of age, using the male breeding value (GBW10m) both in male and female ducks. In a second step the males were selected according to their ability to give semen at semen collection, the females with best laying ability were selected to produce progeny. In CL, in the first step, males and females where chosen, within sire family, when their breeding values were near the mean of the population in G8 and G9 and they were randomly chosen from G10 to G12. In the second step the males were chosen randomly in the male with ability to give semen, the females were chosen randomly within the laying duck. The theoretical experimental procedure was described in Hu (1999).
Statistical analysis
All records were analyzed using the SAS univariate procedure (SAS Institute, 1994), to calculate means and phenotypic standard deviations (sd). The model for the prediction of additive genetic values of the selected trait was as described in Hu et al. (1999): a multivariate analysis with an animal model of BW10m, BW10f, BW18m, BW18f, Fl10m, Fl10f was performed, using the model:
yij=hi+aj+eij
where yij was the performance of the jth animal born in the ith hatch, hi was the fixed effect of the ith hatch, aj the random additive genetic effect of the jth animal, eij the random residual term. In each generation, all the ancestors of the selection candidates back to the founder animals were taken into account to establish the additive genetic relationship matrix; The performances of ducks in all generations (from G0) were also taken into account. The genetic parameters used were shown in Hu et al.(1999). Predicted genetic values were estimated by Pest 4.2 package (Groeneveld and Kovac, 1990), with BLUP applied to an animal model, with a performance file of 11520 animals from G1 to G13, a pedigree file of 14327 animals, by means of Gauss-Seidel iteration for animal effects. The inbreeding coefficients were considered for the additive relationship matrix. For each generation, the means predicted genetic values of each traits were calculated. Starting from the parents selected in G8 of the former selection, this selection experiment with a selected and control line was conducted over 5 generations from 1997 to 2003 (G8 to G13). Theoretically the SL was bred with 20 sires and 100 dams, the CL was bred with 14 sires and 42 dams. Purpose was to maintain the sire origins over the successive generations.
The selection differentials on breeding values of body weight at ten weeks of age in the CL line were calculated in each generation, as differences between the averages of animals chosen as parents and of all animals measured in that generation. They were calculated in order to detect unintentional selection. The cumulated generation selection responses were measured as the differences in the averages of phenotypic performance of animals in the SL and CL lines. Their variances were calculated taking into account the variance of error measurements and genetic drift variance (Falconer and Mackay, 1996). The predicted genetic responses to selection on body weight at 10 weeks of age was estimated from the within generation line difference (SL-CL) for average predicted breeding values of that trait in males (GBW10m). These predicted additive genetic values were calculated in a 6-trait analysis using the BLUP methodology. For simplification, the approximate standard deviations for the generation SL-CL differences were calculated with the variances of the predicted additive genetic values.
Period III: Selection based on the index
During the third period, a selection genetic index for desired gains in the number of eggs laid up to 40 weeks of age and body weight at ten weeks of age was studied. Thus, the goal of this study was to construct the selection indices of dual-purpose selection of body weight at 10 weeks of age and egg production up to 40 weeks of age and apply in Muscovy selection population duck. The experimental ducks of the selected line (SL) and control line (CL) were from the birds of L302 reported by Hu et al., (2002). The management was described in Hu et al. (1993) and Hu (1999). The ducklings were kept on the high-raised wire floor inside the brooder house from 0 to 3 weeks of age and then kept on the floor or wire floor from 3 to 10 weeks of age. After 10 weeks of age, the ducks selected in the first selection step were raised in individual wire cages in a confined or windowless housing , fed a restricted diet containing 14% CP and 2800 kcal/kg ME during growing period, and a diet containing 20% CP and 2800 kcal/kg ME during laying period. Drinking water was provided ad libitum throughout the experiment. Growth performance was individually measured at 10 weeks of age (BW10). Laying performance was individually recorded from the onset of lay. Individual data were calculated for five laying traits: age at first egg (AGE1EGG), number of eggs laid up to 40 and 52 weeks of age (NEGG40 and NEGG52), and number of eggs laid during the first 15 and 22 weeks in the first laying cycle (NEGG15W and NEGG22W).
Selection method
All Muscovy ducks were kept in the way of a small population chosen randomly in CL or selected for individual additive genetic value of body weight at 10 weeks of age at the first step of selection in SL as reported by Hu et al. (2002) from generation 13 (G13) and generation 14 (G14) in I-Lan of Taiwan. In a second step about 20 males and 100 females were selected with the best selection index and the ability to give semen at semen collection in males and the best laying ability in females in SL. They were chosen, within sire families, randomly in those birds with the ability to give semen at semen collection in males and the best laying ability in females in CL.
The heritabilities and genetic correlations of the five laying traits, together with the growth traits (BW10, Fl10 and BW18) which were estimated by a multi-trait REML applied to an animal model were taken from Hu et al. (2004). Predicted breeding values of the eight traits were calculated by an MT-BLUP animal model that accounts for inbreeding using the PEST program (Groeneveld, 1990; Groeneveld and Kovac, 1990; Groeneveld et al., 1992).
Selection index
For obtaining the coefficient of index a0 and a1, according to the classical theory (Rouvier, 1969, 1977; Mallard, 1972), the genetic selection index for multiple trait can be written:
Ig =a’ĝ where a is the vector of coefficients for n breeding values, a’ is a transposed, and ĝ is the vector of predictors of breeding values for each of the n traits, calculated as the multiple regression of g above all the phenotypic predictors, E(ĝ)=0. The multiple correlation between Ig and H=a’g is maximum. H is the aggregate genotype, g is the vector of breeding values with E(g)=0. When selecting by truncation for Ig with intensity of selection i, the expected genetic gain in each trait is given by
EΔg=i/σIg Ba [1]
where EΔg is the expected genetic gain in each trait and the matrix E(ĝĝ’)=B; σIg is the standard deviation of Ig. With the classical selection index (the means are supposed known), the matrix B can be calculated, if the matrix G= E(gg’) is assumed to be known. The correlation between H and Ig is calculated by
R2Hig=a’Ba/a’Ga [2]
According to Lin(1990) followed by Cheng et al.(1996), Chen et al.(2003) who gave the first results of application of restricted genetic index, B can be approximated by which is the matrix of the variances and covariances of the predicted breeding values in an animal model, separately for male and female ducks. Therefore, the standard deviation of I g can be obtained from [2] by
g can be obtained from [2] by
σIg= [3]
[3]
Since i/σIg is constant, it can be dropped without affecting the proportionality of a. Then, restricted genetic selection index coefficients a, or coefficients for desired gains can be obtained from [1] by
a=B-1w [4]
where w is a vector of proportional values for the desired gains of the restricted traits.
New selection criterion adopted a model of Ig =a’ĝ mentioned before. It was combined by two characters and their weighting coefficient, therefore, the index should be I= a0GNEGG40 + a1GBW10, GNEGG40 and GBW10 were referred to the additive genetic value of two characters (NEGG40 and BW10). For calculating the breeding values, the parameters estimated from the first seven generations were used, the variances and covariances of breeding values were calculated by SAS (SAS Institute Inc;1994) from the data of G13 and G14 (issue from the additive genetic values estimated by PEST from 14328 birds of 13 generations and 14852 birds of 14 generations). Then, the restricted genetic selection index coefficients a, the standard deviation of Ig, and the predicted genetic progress were calculated by IML of SAS with the certain ratios of the expected progress of additive genetic values of egg number and body weight, and compared with the trends estimated from the first seven generation.
RESULTS AND DISCUSSION
Period I: Selection based on phenotypic performance and estimation of parameters from G0 to G8
The results will be shown and discussed following Hu (1999) and Hu et al. (1999).Means, standard deviations of the body weights and feather lengths and the ratios of male to female average body weight, and female to male average feather length are given in Table 3.
Table 3. Means and standard deviation ( ± sd) for BW10m, BW10f, Fl10m, Fl10f, BW18m, and BW18f and male to female average body weight ratios (M/F) and female to male average feather length ratios (F/M) over 9 consecutive generations.
± sd) for BW10m, BW10f, Fl10m, Fl10f, BW18m, and BW18f and male to female average body weight ratios (M/F) and female to male average feather length ratios (F/M) over 9 consecutive generations.
Traits unit | BW10m g | BW10f g | M/F | Fl10m cm | Fl10f cm | F/M | BW18m g | BW18f g | M/F |
Generation | | | | | | | | |
0 | 3200 ± 179
| 2135 ± 120
| 1.50 | 14.8 ± 1.7 | 17.0 ± 1.7 | 1.15 | - | - | - |
1 | 2641 ± 352
| 1813 ± 276
| 1.46 | 10.7 ± 3.5 | 13.0 ± 3.0 | 1.21 | - | - | - |
2 | 2738 ± 570
| 1908 ± 341
| 1.44 | 12.7 ± 4.0 | 15.3 ± 3.6 | 1.20 | - | - | - |
3 | 3109 ± 453
| 2135 ± 183
| 1.46 | 13.3 ± 3.6 | 16.2 ± 2.5 | 1.22 | 4465 ±285
| 2550 ± 181
| 1.75 |
4 | 3203 ± 443
| 2177 ± 191
| 1.47 | 16.7 ± 2.3 | 17.7 ± 1.7 | 1.06 | 4862 ± 318
| 2816 ± 192
| 1.73 |
5 | 3064 ± 629
| 2164 ± 252
| 1.42 | 13.3 ± 3.4 | 15.3 ± 2.6 | 1.15 | 4131 ± 392
| 2624 ± 184
| 1.57 |
6 | 2922 ± 546
| 2054 ± 319
| 1.42 | 14.6 ± 2.2 | 16.4 ± 1.6 | 1.12 | 4611 ± 423
| 2744 ± 189
| 1.68 |
7 | 3692 ± 318
| 2334 ± 163
| 1.58 | - | - | - | - | - | - |
8 | 3195 ± 462
| 2157 ± 214
| 1.48 | - | - | - | - | - | - |
BW10m, BW10f, body weights at 10 weeks of age, male and female.
Fl10m, Fl10f, 8th primary feather length at 10 weeks of age, male and female. BW18m, BW18f, body weights at 18 weeks of age, male and female.
The mean of the body weight decreased in generations 1 and 2, and increased afterwards. The similar trend was observed for feather lengths. The 8th primary feather is longer in females than in males by 6-22 % at 10 weeks of age. Body weight is heavier in males than in females by 42-58 % at 10 weeks of age and by 57-75 % at 18 weeks of age.
The means, standard deviation, minimum and maximum of inbreeding coefficients are given in Table 4. The birds of G0 were assumed to be neither related nor inbred. Inbreeding coefficients increased in G2 due to some full sibs in G1, and after decreased to an average per generation of 6% to 7%.
Estimates of additive genetic parameters, phenotypic correlations and phenotypic standard deviations are given in Table 5. Heritabilities of body weight at 10 and 18 weeks of age for male and female were in the range 0.24 to 0.43 and those of feather lengths for male and female were 0.37 and 0.14, respectively. Heritabilities of sexual dimorphism were 0.07, 0.10 and 0.10 respectively for body weight at 10 weeks and 18 weeks of age and for feather length at 10 weeks of age.
Table 4. Means, standard deviation, minimum and maximum of inbreeding coefficients % of Muscovy L302 in each generation G0 to G8.
Generation | Number of ducks | Mean
±standard deviation % | Minimum % | Maximum % |
G0 | 38 | 0 | 0 | 0 |
G1 | 187 | 0 | 0 | 0 |
G2 | 829 | 1.2±5.3
| 0 | 25.0 |
G3 | 1036 | 2.5±3.5
| 0 | 25.0 |
G4 | 1096 | 5.6±3.7
| 0 | 28.1 |
G5 | 1108 | 5.5±2.5
| 0 | 28.5 |
G6 | 799 | 6.2±2.0
| 0 | 11.4 |
G7 | 775 | 6.4±2.6
| 0 | 12.9 |
G8 | 721 | 5.1±3.6
| 0 | 12.5 |
Table 5. Heritabilities, phenotypic and genetic correlations among the 6 traits, phenotypic standard deviations (std) of the 6 traits.
Traits unit | BW10m g | BW10f g | Fl10m cm | Fl10f cm | BW18m g | BW18f g |
BW10m | 0.24 (0.03) | 0.90 (0.04) | 0.75 (0.04) | 0.80 (0.06) | 0.77 (0.05) | 0.59 (0.06) |
BW10f | | 0.31 (0.03) | 0.59 (0.05) | 0.77 (0.05) | 0.81 (0.04) | 0.80 (0.04) |
Fl10m | 0.60** | | 0.37 (0.04) | 0.88 (0.05) | 0.23 (0.07) | 0.14 (0.06) |
Fl10f | | 0.46** | | 0.14 (0.02) | 0.51 (0.09) | 0.47 (0.08) |
BW18m | 0.21** | | 0.17** | | 0.36(0.04) | 0.89 (0.04) |
BW18f | | 0.11** | | 0.10* | | 0.43 (0.04) |
std | 408 | 217 | 3.15 | 2.5 | 322 | 191 |
BW10m, BW10f, body weights at 10 weeks of age, male and female.
Fl10m, Fl10f, 8th primary feather length at 10 weeks of age, male and female. BW18m, BW18f, body weights at 18 weeks of age, male and female.
Heritabilities are given on the diagonal, genetic correlations above diagonal, phenotypic correlations below diagonal.
(): Standard errors of the estimates
*:Significant (P < 0.05),** Highly significant (P < 0.01)
Genetic trends for the six traits are reported in Fig 1. As the scale of measure varied according to the trait, the genetic level was expressed per unity of genetic standard deviation (σg) which was estimated to be 201 g for BW10m, 121 g for BW10f, 1.93 cm for Fl10m, 0.96 cm for Fl10f, 194 g for BW18m and 125 g for BW18f. The genetic levels for BW10m and BW10f seem to decrease from G0 to G1, but not significantly. The genetic levels for body weights at 10 weeks of age in males and females increase from G2. The genetic trends seemed to be not linear. It was preferred to calculate the predicted genetic progress from each generation to the following and to cumulate over the eight generations of selection, instead of estimating the regression equation of the averaged predicted genetic values over the generation number. The cumulated predicted genetic gains after 8 generations of selection were similar, like expected, for BW10m (1.3 σg) and BW10f (1.4 σg). The correlated predicted responses were equal in males and females for the body weights at 18 weeks of age, being 1.2 σg. The predicted correlated genetic responses in Fl10f and Fl10m were less (0.9 σg and 0.7 σg , respectively).

Fig 1. The genetic trends standardized by the genetic standard deviation of BW10m, BW10f, Fl10m, Fl10f, BW18m and BW18f.
Genetic parameters
First estimates of the body weight heritabilities were based on the sire, dam within sire, or sire+dam variance components, respectively h2s, h2d, h2s+d. Ricard et al. (1983) found heritabilities of body weight at 10 weeks of age in Muscovy of 0.24 (h2s), and 0.62 (h2d) in male, of 0.47 (h2s) and 0.49 (h2d) in female. Pingel (1990) quoted values of heritabilities (sire + dam variance components) from 0.43 to 0.53 for body weight at 70 and 74 days, in male or female progeny. Poujardieu et al. (1994) compiled values of heritabilities of body weights at 53 days up to 84 days of age, ranging at 0.17 to 0.55, for male Muscovy ducks which were force fed. These estimates were obtained by using the variance components estimation with the model sire and dam nested within sire. In this case, the full relationship matrix between all individuals was not taken into account and results may be biased, especially in selected populations (Poujardieu et al., 1994).
In our case the body weight heritabilities were of moderate values, being for body weight at 10 weeks of age of h2 = 0.24 and h2 = 0.31, respectively for males and females, and for body weight at 18 weeks of age, of h2 = 0.36 in males, of h2 = 0.43 in females. The heritabilities increased with age. They seemed to be a little larger in females than in males, as found by Chapuis et al. (1996) for turkeys and Mignon-Grasteau et al. (1998) for Muscovy. They interpreted that result by the more precocious growth of females which at a given age are more mature than males and so differ in their body composition and percentage of fat tissue which is very heritable.
On the contrary, the heritability of Fl10m (h2 = 0.37) is higher than that of Fl10f (h2=0.14). That is due to a much lower additive genetic variance of feather length in females than in males (σ2g =0.92 versus σ2g =3.71). It would be interesting to measure feather length at a later age, in order to determine whether the feathers are still growing in adult males and females.
Mignon-Grasteau et al. (1998) found high values of the heritability for the juvenile body weight in the Muscovy duck. They were h2 = 0.40, h2 = 0.51 for body weight at 6 weeks of age respectively in males and females. They found for weight gain between 6 weeks of age and slaughtering age, h2 = 0.33 and h2 = 0.67 respectively in males and females.
Subtropical climate with no controlled environment could act both to decrease the body weight means and increase the phenotypic variances. Hester et al. (1981) reported that weight gain at 52 days of age in Pekin duck was decreased at high temperature (29.4º) compared to temperate one (18.3º) while feed consumption remained constant. Yahav et al. (1998) found that high relative humidity (RH above 75%) at high ambient temperature deteriorated the growth performances between 10 and 15 weeks of age in turkey may be due to severe respiratory alkalosis. The coefficients of variation based on all generation found in this population were 18% and 13% in male and female, respectively. They are greater than those calculated in Europe, for example 5.8% to 9.5% at 10 weeks of age and 5.7% to 14.5% at 12 weeks of age in male Muscovy, calculated from the data reported from Baeza et al. (1997) and Beaumont et al. (1997). At the same age, Paci et al.(1993) reported coefficient of variation of 6.3% to 8.3% in male and 10% in female, Ricard et al. (1983) reported 10% in male and 8% in female. In subtropical climate, due to variability of response to climatic effects, a higher residual variance could be expected and so lower values of the heritability.
The heritabilities of the differences between male and female body weights were lower than those estimated by Mignon-Grasteau et al. (1998) in the Muscovy and than those reported by Chapuis et al. (1996) for turkeys. In that population and environment, it would be difficult to modify the sexual dimorphism of body weight by selection. It was assumed that sexual dimorphism was at least partly caused by some genes carried by the sexual chromosome (Merritt, 1966; Bernon and Chambers, 1985). It was usually considered as a fixed effect in chicken (Koerhuis and Thompson, 1997), in turkey (Toelle et al., 1990). Dominance effects from the sex-linked genes on the Z chromosome may be expressed in males, and not in females. Besides, Kharel and Arboleda (1986) indicated that the sexual dimorphism of Muscovy body weight was attributed in part to the effect of sex-linked as well as autosomal genes. Recently, Tai and Rouvier (1998), in a factorial crossbreeding experiment between Muscovy and Pekin ducks, suggested that besides the effects of sex-linked genes, assumed coding genes of the non-pseudo-autosomal region (NPAR) of the Muscovy W chromosome, compared to those of the Pekin W chromosome, appear to depress growth.
The genetic correlations between sexes for body weight at the same age were rg=0.9±0.04 at 10 weeks of age, and similar with 0.89±0.04 at 18 weeks of age. Although very high, they seem to be significantly different from 1. They were higher than the genetic correlations between ages in the same sex. The genetic correlation between sexes for the feather length were also high (rg = 0.88±0.05). Fl10f was genetically correlated with the BW10m (rg = 0.8) and the BW10f (rg = 0.77), and so the Fl10m with little less values of the genetic correlations.
Mignon-Grasteau et al. (1998) found a genetic correlation rg = 0.85 between both sexes in Muscovy at 6 weeks of age. But, unlike our results, they indicated that the correlation between body weights of both sexes at 10 weeks of age was 0.72 only. Moreover, Chapuis et al. (1996) found for 3 strains of turkeys, average genetic correlations between body weights of both sexes of 0.90 at 12 weeks of age and of 0.85 at 16 weeks of age, only a little inferior to the genetic correlation between ages (0.95 for females and 0.93 for males). Le Bihan-Duval et al. (1998) found in chickens very high genetic correlations between traits at the same age (0.95 for body weight at 6 weeks of age).
The high body weight sexual dimorphism in the Muscovy duck, increasing with age, observed in our data, was well known (Leclercq, 1990, Leclercq and de Carville, 1986). The high genetic correlation between sexes suggests that sex linked genes express few and control little variation in these traits. The genetic and residual variances are very different in both sexes. Further, in the case of genetic correlation inferior to 1, the measurements from two sexes at the same chronological age may be measuring different physiological traits. When the body weights at the same age in male and female are considered as separate traits, the question may arise of how to combine the two separate predicted genetic values got for each sex by the BLUP animal model. According to the Taiwanese objectives, the genetic levels of 10 weeks body weights for both male and female have to be increased. One objective in a first time could be to evaluate each bird, male and female, by the average of the two predictors, giving equal importance to the body weights in each sex.
In this study, we wanted to determine whether feather length was a heritable character in order to know if possible in the future to select for rapid feather growth for easier defeathering after slaughtering. It seems better to select on the body weight at 10 weeks of age and to take advantage of the expected correlated response of feather length.
Genetic trends
When there is no control population, the genetic response per generation can be obtained by the regression of the average predicted genetic values of the ducks of the same generation on generation number (Cheng et al., 1996). This method to estimate genetic trends is unbiased because the genetic evaluation is based on a multitrait animal model (Henderson, 1975; Ducrocq, 1994). The predicted genetic response depends on the genetic parameters which have been used (Thompson, 1986). They were obtained here as unbiased estimates in the base population, neglecting the maternal effects.
The mean of the predicted genetic values were statistically equal to 0 in the G0, as expected. Their apparent decrease from G0 to G1 could be explained by random deviation, and because the realized selection intensity on the 10 weeks body weight in selecting the parents for G1 was near 0 (i=0.08 on average for males and females) and the population size was small. In G2, the increase of the inbreeding coefficients could counteract partly the effects of the selection which was made in G1. From G2 up to G8, the genetic levels of body weights at 10 weeks of age increased in these 6 generations of selection, of 1.4 σg. When comparing in farms raising Muscovy ducks for meat, Muscovy L302 from G6 and local ones, Hu et al. (1999) found significant differences in body weights at 10 weeks of age, in favor of the L302.
Although there was no control line, it seems that the selection was successful to improve growth rate up to 10 weeks of age, and the correlated traits, especially from the G2 when the population size was increased.
Period II: Selection based on the additive genetic values and setting up a control line
From G9 to G13, 2341 male, 2293 female ducks were measured in SL line, 612 male and 654 female ducks were measured in CL line. The average male and female per generation selection differentials on predicted breeding values were 48.4 in SL and 9.4 in CL (Table2). Thus there was unintentional selection in the CL line.
Table 6 shows the means and standard deviations of body weight at 10 weeks of age and of the additive genetic value of animals of the population from G8 to G13.
Table 6. Means ± standard deviation of body weight (g) at 10 weeks of age (BW10) and of its predicted additive genetic value (GBW10m) of population from G9 to G13
| | SL | CL |
Gener | Sex | No | BW10 | GBW10M | No | BW10 | GBW10M |
G8 | M | 476 | 2752±416 | 88±104 | 476 | 2752±416 | 88±104 |
G9 | | 341 | 3681±257 | 151±66 | 116 | 3618±273 | 102±62 |
G10 | | 532 | 3486±315 | 157±88 | 178 | 3507±257 | 129±80 |
G11 | | 309 | 3719±430 | 219±100 | 91 | 3638±344 | 142±94 |
G12 | | 419 | 3872±404 | 253±91 | 134 | 3715±390 | 132±113 |
G13 | | 264 | 4131±353 | 320±73 | 93 | 3958±320 | 139±108 |
| | | | | | | |
G8 | F | 504 | 1897±229 | 87±109 | 504 | 1897±229 | 87±109 |
G9 | | 311 | 2329±149 | 152±68 | 158 | 2309±157 | 105±68 |
G10 | | 509 | 2337±140 | 158±92 | 186 | 2320±139 | 123±75 |
G11 | | 360 | 2460±180 | 207±107 | 76 | 2446±142 | 153±105 |
G12 | | 401 | 2540±181 | 250±85 | 132 | 2489±154 | 155±105 |
G13 | | 208 | 2528±160 | 322±71 | 102 | 2468±205 | 164±128 |
M: male; F: female; No: number of animals
SL: Selection line; CL: Control line
The observed selection response means have large standard deviations. Selection response of body weight at ten weeks of age of males in G13 is significant (P<0.05), but not for females (0.1<P<0.2). The genetic progress was underestimated because there was an unintentional selection of the control line. The predicted genetic responses from BLUP under an animal model were less variable, as expected, and seem to be significant. From G0 to G5, the genetic levels of body weight at 10 weeks of age increased along the 5 generations of selection from 88 to 320 and from 87 to 322, in male and female ducks respectively in LS line. The genetic levels increased by 0.23σg and by 0.39σg on average per generation of selection in male and female duck respectively of SL line.
Period III: Selection based on the index
Upon considering the component of the indices, the number of eggs laid up to 40 weeks of age was chosen with body weight at 10 weeks of age instead of the number of eggs laid up to 52 weeks of age to keep one year of generation interval. According to this selection object, the desired gains (w) were proposed arbitrarily in Table 7 and 8. In consequence, the results of calculation of the restricted genetic selection indices coefficients (a0, a1), respectively for number of eggs laid up to 40 weeks of age and body weight at 10 weeks of age, the standard deviation and expected genetic gains in male and female ducks with selection intensity i=1 in G13 and G14 were shown in Table 7 and 8.
Table 7. Desired gains, restricted genetic selection indices coefficients, the standard deviation and expected genetic gains in male and female ducks with selection intensity i=1 in G13.
Sex | No | w' | a0 | a1 | σIg | (EΔg)’ |
Male | 1 | 1, 50 | 0.3933 | 0.0078 | 0.8864 | 1.1281 | 56.4061 |
| 2 | 1, 100 | 0.5357 | 0.0129 | 1.3493 | 0.7411 | 74.1109 |
| 3 | 1, 200 | 0.8204 | 0.0229 | 2.3219 | 0.4307 | 86.1377 |
| | | | | | | |
Female | 1 | 1, 50 | 0.3918 | 0.0078 | 0.8864 | 1.1281 | 56.4061 |
| 2 | 1, 100 | 0.5390 | 0.0127 | 1.3466 | 0.7426 | 74.260 |
| 3 | 1, 200 | 0.8334 | 0.0225 | 2.3113 | 0.4327 | 86.5324 |
Table 8. Desired gains, restricted genetic selection indices coefficients, the standard deviation and expected genetic gains in male and female ducks with selection intensity i=1 in G14.
Sex | No | w’ | a0 | a1 | σIg | (EΔg)’ |
Male | 1 | 1, 50 | 0.1822 | 0.0098 | 0.8200 | 1.2195 | 60.9747 |
| 2 | 1, 100 | 0.2375 | 0.0185 | 1.4449 | 0.6921 | 69.2079 |
| 3 | 1, 200 | 0.3481 | 0.0359 | 2.7437 | 0.3645 | 72.8931 |
Female | 1 | 1, 50 | 0.1366 | 0.0086 | 0.7522 | 1.3295 | 66.4739 |
| 2 | 1, 100 | 0.2021 | 0.0159 | 1.3371 | 0.7479 | 74.7903 |
| 3 | 1, 200 | 0.3331 | 0.0304 | 2.5326 | 0.3949 | 78.9717 |
CONCLUSION
Under Taiwanese climatic conditions the heritabilities of Muscovy male and female body weights at 10 weeks and 18 weeks of age, and of feather length in males at 10 weeks of age, were of moderate values. These traits could be altered by selection. Further investigations are needed to explain the genetic basis of body weight sexual dimorphism and to estimate the genetic parameters taking into account the maternal effects. The genetic levels for the body weights at 10 weeks of age were increased by the selection, and so for the correlated traits. It was concluded that it seems worthwhile to continue that selection experiment, considering separate male and female body weight at 10 weeks of age and establishing an unselected control line to estimate the realized genetic progress by the response to selection.
The results show a significant selection response of body weight at 10 weeks of age in male after the fifth generation of selection but not in female duck. So it should be worthwhile to continue that selection experiment for some generations in order to show the genetic progress which could be reached under tropical conditions.
It was suggested to choose 1:100 as the ratio of desired genetic gains for selection line L302S, on expecting moderate improvement in both the number of eggs laid up 40 weeks of age and the body weight at 10 weeks of age in L302S. For control line, no selection index was used. These indices will be applied for the selection of the growth and laying performances. It would be worthwhile to continue the experiment and to analyze further the efficiency of response of index after at least three generations of application.
ACKNOWLEDGMENTS
This study was undertaken as a cooperative research project by the Council of Agriculture-Taiwan Livestock Research Institute and the Institut National de la Recherche Agronomique. We are indebted to the staff of the I-Lan Branch of the Livestock Research Institute (LRI) for carrying out this research and collecting the data, and to the Institut National de la Recherche Agronomique, Station d'Amélioration Génétique des Animaux du Département de Génétique Animale (INRA-SAGA) and Council of Agriculture for scientific advice and financial support.
REFERENCES
Babilé, R. 1989. La production de foie gras de canards de Barbarie (Cairina moschata) : aspects génétiques, nutritionnels et technologiques. Thèse, Institut Polytechnique de Toulouse, France.
Baeza, E., H. de Carville, M. R. Salichon, G. Marche, and B. Leclercq. 1997. Effects of selection, over three and four generations, on meat yield and fatness in Muscovy ducks. British Poultry Science, 38: 359-365.
Beaumont, C. 1992. Genetic parameters of the duration of fertility in hens. Canadian Journal of Animal Science, 72: 193-201.
Beaumont, C., E. Le Bihan-Duval, and B. Desnoues. 1997. Genetic parameters of leg disorders in Muscovy ducks. Proceedings of the 11th European Symposium on Waterfowl, World's Poultry Science Association, Tours, France, pp. 264-268.
Bernon, D.E. and J. R. Chambers. 1985. Maternal and sex-linked effects in broiler parent stocks. Poultry Science, 64: 29-38.
Boichard, D. 1998. Logiciel d'analyse de généaologies adapté aux grandes populations. pp. 1-13. Institut National de la Recherche Agronomique, Paris.
Chapuis, H., M. Tixier-Boichard, Y. Delabrosse, and V. Ducrocq. 1996. Multivariate restricted maximum likelihood estimation of genetic parameters for production traits in three selected turkey strains. Genetics Selection Evolution, 28: 299-317.
Chen, D. T., S. R. Lee, Y. H. Hu, C. C. Huang, Y. S. Cheng, C. Tai, J. P. Poivey, and R. Rouvier. 2003. Genetic trends for Laying Traits in the Brown Tsaiya (Anas platyrhynchos) Selected with Restricted Genetic Selection Index. Asian-Aust. J. Anim. Sci. 2003. 16( 12) : 1705-1710.
Cheng, Y. S., R. Rouvier, J. P. Poivey, and C. Tai. 1995. Genetic parameters of body weight, egg production and shell quality traits in the Brown Tsaiya laying duck. Genetics Selection Evolution, 27: 459-472.
Cheng, Y. S., J. P. Poivey, R. Rouvier, and C. Tai. 1996. Prediction of genetic gains in body weight, egg production and shell quality traits in the Brown Tsaiya laying duck (Anas platyrhynchos). Genetics Selection Evolution, 28: 443-455.
Ducrocq, V. 1994. Multiple trait prediction: principles and problems. . Proceedings of the 5th World Congress on Genetics Applied to Livestock Production, University of Guelph, Guelph, Ontario, Canada, Vol.18, pp. 455-462.
Falconer, D. S. 1952. The problem of environment and selection. American Naturalist, 86: 293-298.
Falconer, D. S. and T. F. C. Mackay. 1996. Introduction to quantitative genetics. Longman, Hong-Kong.
Fedeli Avanzi, C. and R. D. Crawford. 1990. Mutations and Major variants in Muscovy ducks. In. Poultry breeding and genetics, pp. 389-394 (Crawford R.D. Ed). Elsevier Science Publishing Company Inc, New-York.
Groeneveld E., 1990. PEST user's manual. Department of Animal Science, University of Illinois, Urbana, Illinois, U.S.A
Groeneveld E., M. Kovac, T. L. Wang, and R. L. Fernando. 1992. Computing algorithms in a general purpose BLUP package for multivariate prediction and estimation. Arch. Tierz., 35:399-412
Groeneveld, E. and M. Kovac. 1990. A generalized computing procedure for setting up and solving mixed linear models. Journal of Dairy Science, 73: 513-531.
Groeneveld, E. 1994a. VCE - a multivariate multimodel REML (co)variance component estimation packages. Proceedings of the 5th World Congress on Genetics Applied to Livestock Production, University of Guelph, Guelph, Ontario, Canada, Vol. 22, pp. 47-48.
Groeneveld, E. 1994b. A reparameterization to improve numerical optimization in multivariate REML (co)variance component estimation. Genetics Selection Evolution, 26: 537-545.
Groeneveld, E. 1996. REML VCE a multivariate multimodel restricted maximum likelihood (co)variance component estimation package. Version 3.2 User's Guide.
Henderson, C. R. 1975. Best linear unbiased estimation and prediction under a selection model. Biometrics, 31: 423-477.
Henderson, C. R. 1988. Theoretical basis and computational methods for a number of different animal models. Journal Dairy Science, 71 (suppl. 2): 1-16.
Hester, P. Y., F. W. Pierson, E. K. Wilson, R. L. Adams, and W. J. Stadelman. 1981 Feed/gain ratios of White Pekin ducks as affected by age and environmental temperature. Poultry Science, 60: 2401-2406.
Hill W. G., 1972. Estimation of realized heritabilities from selected experiments. II. Selection in one direction. Biometrics, 28:767-780
Hu Y. H., T. H. Tseng, S. R. Lee, Y. N. Jiang, T. C. Chen, and C. Tai. 1993. Selection for large body size of Muscovy. I. Foundation stock in Taiwan. Taiwan Livestock Research, 26: 285-295.
Hu, Y. H. 1999. Variabilité génétique des performances de croissance et de ponte dans une lignée de canards de Barbarie sélectionnée à Taiwan ; Viabilité embryonnaire précoce dans le croisement intergenerique des canards.thèse de doctorat. Institut National Polytechnique de Toulouse. France .
Hu, Y. H., J. P. Poivey, R. Rouvier, C. T. Wang, and C. Tai. 1999. Heritabilities and genetic correlations of body weights and feather length in growing Muscovy selected in Taiwan. British Poultry Science, 40:605-612.
Hu, Y. H., C. T. Wang, and C. Tai. 1999. Selection for large body size of Muscovy. II. Meat Muscovy growth performance test. Taiwan Livestock Research, 32 (1):63-70。
Hu, Y. H., J. P. Poivey, R. Rouvier, A. J. F. Huang, C. T. Wang, and C. Tai. 2002. Estimation of genetic gains in Muscovy duck selected for body weight at ten weeks of age in Taiwan. Proceeding of 7th World Congress on Genetics Applied to Livsestocks Production. 30:269-272.
Hu, Y. H., J. P. Poivey, R. Rouvier, R., S. C. Liu, and C. Tai. 2004. Heritabilities and genetic correlations of laying performances in Muscovy selected in Taiwan. British Poultry Science, 45:180-185.
Im, S., R. L. Fernando, and D. Gianola. 1989. Likelihood inference in animal breeding under selection : a missing data theory view point. Genetics Selection Evolution, 21: 399-414.
Kennedy, B. W. 1990. Use of mixed model methodology in analysis of designed experiments. In. Advance in Statistical Methods for Genetics Improvement of Livestock, pp. 77-97 (Gianola, D. and K. Hammond Eds). Springer-Verlag, Berlin.
Kharel, M. and C. R. Arboleda. 1986. Some genetic factors responsible for body growth in Muscovy duck. Journal of the Institute of Agriculture and Animal Science, Nepal, 7: 101-110.
Koerhuis, A. N. M., and R. Thompson. 1997. Models to estimate maternal effects for juvenile body weight in broiler chickens. Genetics Selection Evolution, 29: 225-249.
Le Bihan-Duval, E., S. Mignon-Grasteau, N. Millet, and C. Beaumont. 1998. Genetic analysis of a selection experiment on increased body weight and breast muscle weight as well as on limited abdominal fat weight. British Poultry Science, 39: 346-353.
Leclercq, B. and H. de Carville. 1986. Growth and body composition of Muscovy ducks. In. Duck Production Science and World Practice, pp. 102-109 (Farrell D.J. and P. Stapleton Eds). University of New England, Armidale, Australia.
Leclercq, B. 1990. Croissance et composition corporelle du canard de Barbarie. In. Le canard de Barbarie, pp. 169-193 (Sauveur, B., and H. de Carville Eds). INRA, Paris.
Lin, C. Y. 1990. A unified procedure of computing restricted best linear unbiased prediction and restricted selection index. J. Anim. Breed. Genet. 107:311-316.
Mallard, J. 1972. La theorie et le calcul des index de sélection avec restrictions: synthese critique. Biometrics 28:713-735.
Merritt, E. S. 1966. Estimates by sex of genetic parameters for body weight and skeletal dimensions in a random bred strain of meat type fowl. Poultry Science, 45: 118-125.
Meyer, K. 1992. Bias and sampling covariances estimates of variance components due to maternal effects. . Genetics Selection Evolution, 24:487-509.
Mignon-Grasteau, S., C. Beaumount, J. P. Poivey, and H. de Rochambeau. 1998. Estimation of the genetic parameters sexual dimorphism of body weight in 'label' chickens and Muscovy ducks. . Genetics Selection Evolution, 30:481-491.
Paci, G., M. Bagliacca, M. Marzoni, and C.F. Avanzi. 1993. Quality of Italian strains of Muscovy, common and Muscovy x common ducks bred under two different technologies. Proceedings of the 11th European Symposium on Poultry Meat Quality, World's Poultry Science Association, Tours, France, pp. 66-73.
Pingel, H. 1990. Genetics of growth and meat production in waterfowl. In. Poultry Breeding and Genetics, pp. 691-704 (Crawford R.D. Ed). Elsevier, Amsterdam.
Poujardieu, B., F. Guichard, and P. Laventure. 1994. Paramètres génétiques de croissance et de gavage de la cane commune. Genetics Selection Evolution, 26: 463-472.
Ricard, F.H., B. Leclercq, and H. de Carville. 1983. Mise au point sur les caracteristiques genetiques et les methodes d'elevage du canard de Barbarie. Annales de Zootechnie, 32: 189-200.
Rouvier, R. 1969. Pondération des valeurs génotypiques dans la sélection par index sur plusieurs caractères. Biometrics 25: 295-307.
Rouvier, R. 1977. Mise au point sur le modéle classique d'estimation de la valeur génétique. Ann. Génét. Sél. Anim. 9(1) : 17-26.
SAS Institute Inc. (1999) SAS/STAT User’s Guide, Version 8, 1rd Edition. SAS Institute Inc., Cary, NC.
Shaeffer, L. R.1984. Sire and cow evaluation under multiple trait models. J. Dairy Sci. 67, 1567-1580.
Szejniuk, B. and J. P. Kluczek. 1985. Environmental factors effect on the health and productivity of the Muscovy duck. Proceedings of the V Internationaler Kongress fur Tierhygiene, Hannover, German. (Abstr).
Tai, C., C. L. Kang, S. R. Lee, B. J. Chen, and J. J. L. Tai. 1984. Comparisons of growth and egg production among crosses of local breeds and crosses of imported common ducks. J. Chin. Soc. Anim. Sci., 13: 53-61.
Tai, C. 1985. Duck breeding and artificial insemination in Taiwan. In. Duck Production Science and World Practice, pp. 193-203 (Farrell D.J. and P. Stapleton Eds). University of New England, Armidale, Australia.
Tai, C., T. H. Tseng, M. C. Chen, Y. N. Jiang, and H. H. Huang. 1987. The economic performances of Muscovy in Taiwan. Taiwan Livestock Research, 20: 67-71.
Tai, C. and R. Rouvier. 1998. Crossbreeding effect on sexual dimorphism of body weight in intergeneric hybrids obtained between Muscovy and Pekin duck. Genetics Selection Evolution, 30: 163-170.
Thompson, R. 1986. Estimation of realized heritability in a selected population using mixed model methods. Genetics Selection Evolution, 18:475-484.
Thompson, R. and K. Meyer.1986. A review of theoretical aspects in the estimation of breeding values for multitrait selection. Livest Prod. Sci., 15:299-313.
Tixier-Boichard, M., D. Boichard, E. Groeneveld, and A. Bordas. 1995. Restricted maximum likehood estimates of genetic parameters of adult male and female Rhode Island Red Chickens divergently selected for residual feed consumption . Poultry Science, 74: 1245-1252.
Toelle, V. D., G. B. Havenstein, K. E. Nestor, and W. L. Bacon. 1990. Estimates of genetic parameters in Turkeys. 3. Sexual dimorphism and its implications in selection procedures. Poultry Science, 69: 1634-1643.
Van Raden, P. M. 1992. Accounting for inbreeding and crossbreeding in genetic evaluation for large populations. Journal Dairy Science, 75: 3136-3144.
Yahav, S., I. Plavnik, M. Rusal, and S. Hurwitz. 1998. Response of turkeys to relative humidity at high ambient temperature. British Poultry Science, 39: 340-345.